催化工作里的计算案例，来三篇给力的操作！

本文转载自研之成理（ID：rationalscience）

1.  J. Phys. Chem. Lett.,  2017,  8,  1157 – 1160

【领域】：催化 —> 电催化 —> 水的氧化（oxidation of water） 

【问题】：如何调控水氧化产物的选择性？（有三种氧化产物：一电子过程—>OH自由基，二电子过程—>过氧化氢（H2O2），四电子过程—>氧气） 

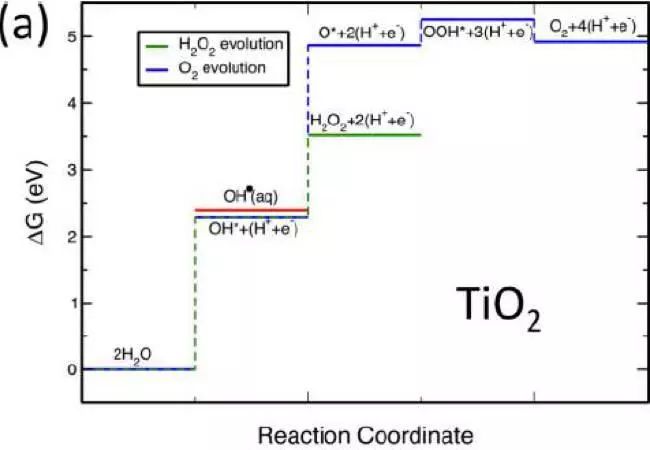
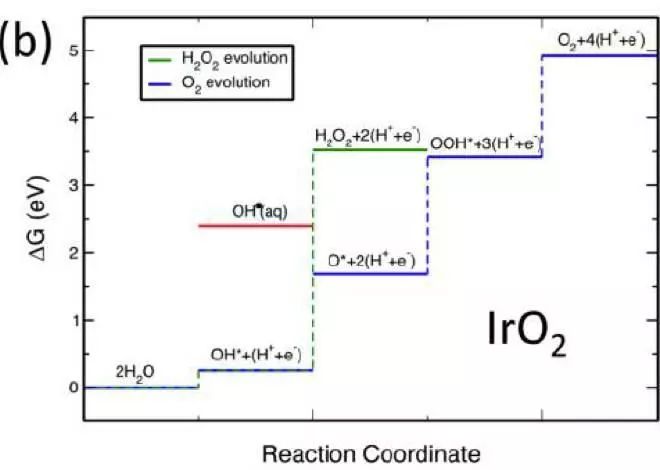
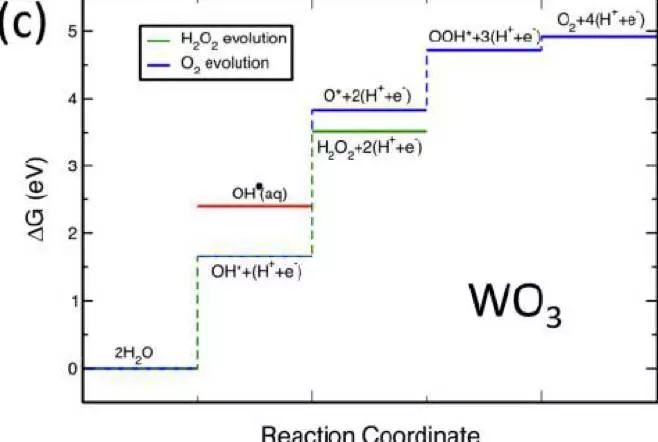
【方法】：作者采用了三个体系（TiO2(110), IrO2(110), WO3(100)），并分别对三个体系计算了反应能量的变化。 

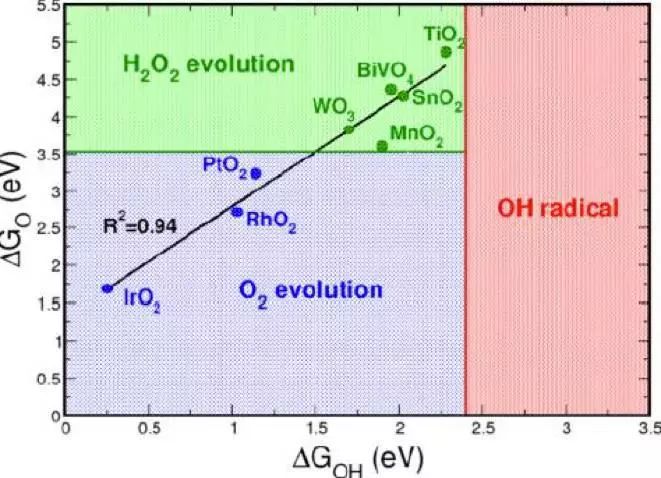
【结论】：当一个催化剂对O的吸附能大于3.5eV，同时对OH的吸附能小于2.4eV时，对过氧化氢的选择性会提高。（能量参考点为G(H2O) = 0, G(H2) = 0） 

【重要图例】：

图1. TiO2(110)表面上各个吸附结构能量变化

图2. IrO2(110)表面上各个吸附结构能量变化

图3. WO3(100)表面上各个吸附结构能量变化

 图4. 在不同催化剂表面上生成三种不同氧化物的条件（绿色为过氧化氢、蓝色为氧气，红色为OH自由基）

【小编点评】：本文指的学习有：（1）其热力学计算方法。（2）给我们展示了一条如何处理“选择性”问题的路线。 

 2. Angew. Chem. Int. Ed., 2017, 56, 3621 – 3624

【领域】：催化—> 电催化 —> CO还原

【问题】：当CO在Cu(100)上还原形成C2化合物时，经过的中间活性物是什么？

【方法】：运用光谱学方法（FTIR）在LiOH溶液中检测C2化合物，并运用DFT计算（VASP-PAW_PBE）对所得到的频率进行比对分析。 

【结论】：CO在还原条件下生成CO-dimer只在Cu(100)面上，而在Cu(111)面上则不会生成。这个原因是由于Cu(100)具有正方形的activesite，可以稳定CO-dimer。有关正方形活性位点可以参考这篇文献：（Li H. J. et al., J Am Chem Soc 2014, 136 (44),15694-15701.）。 

【重要图例】：

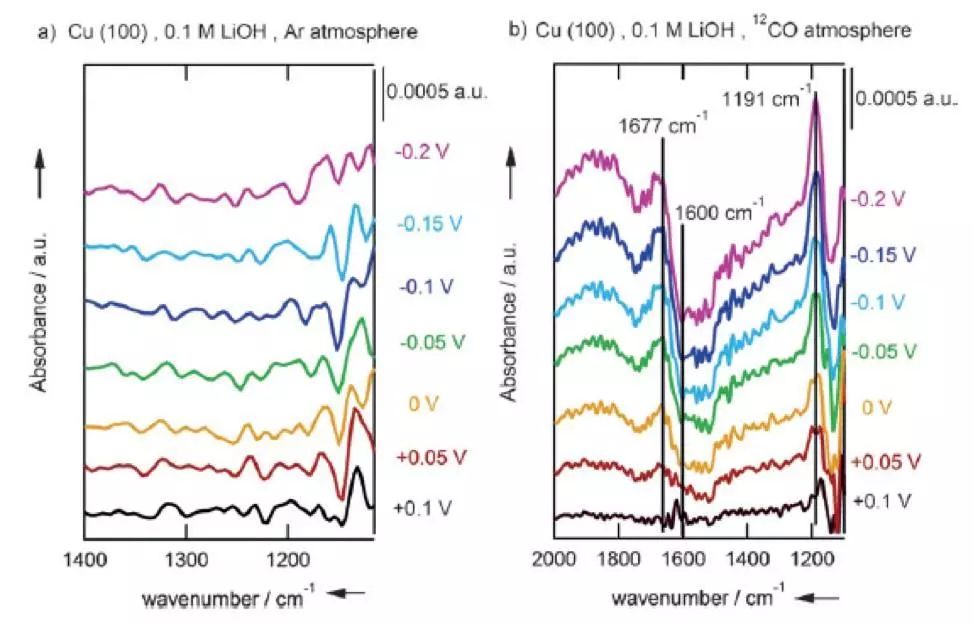
图1. (a)在Ar气氛中不同电势下运用FTIR对体系进行检测 (b)在CO存在下在不同电势中运用FTIR对体系进行检测。1191cm-1的峰是：C(12)-OH的伸缩振动；1677cm-1的峰是：C(12)=O双键的伸缩振动；1600cm-1的峰是O-H的弯曲振动。

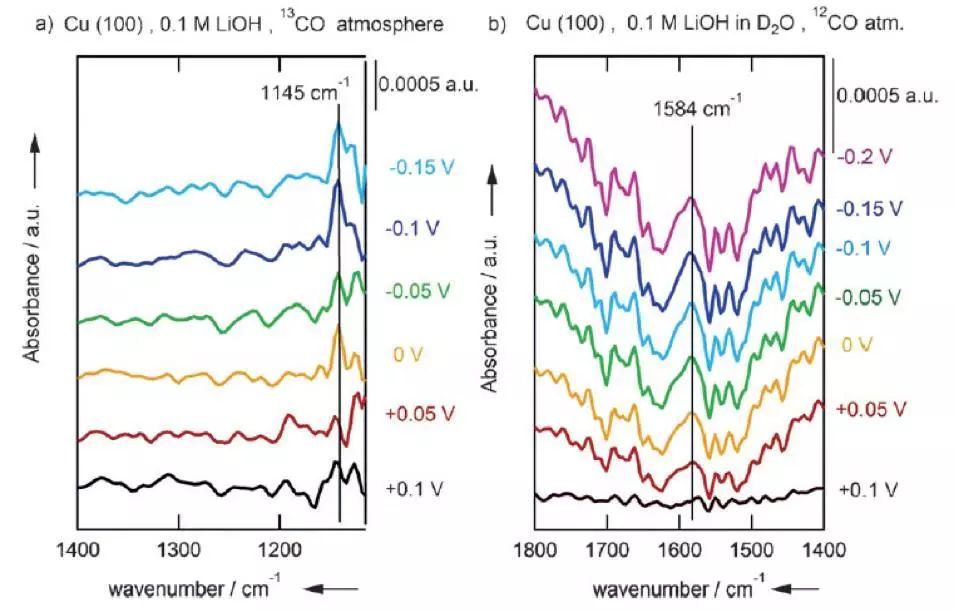
图2. (a)在CO(C13)气氛中，不同电极电势下体系的FTIR谱图（b）在CO(C12)气氛中，不同电极电势下体系的FTIR谱图。其中水换成了重水（D2O）（a）中1145cm-1频率是C13-OH的伸缩振动；（b）中的1584cm-1频率是C12=0的伸缩振动。

因此目前我们有如下的振动频率：1145cm-1(C13-OH伸缩振动)、1191cm-1（C12-OH伸缩振动）、1584cm-1（C12=O伸缩振动）、1600cm-1（O-H的弯曲振动）、1677cm-1（C12O的伸缩振动） 

经过DFT计算不同体系的振动频率可以得到： 

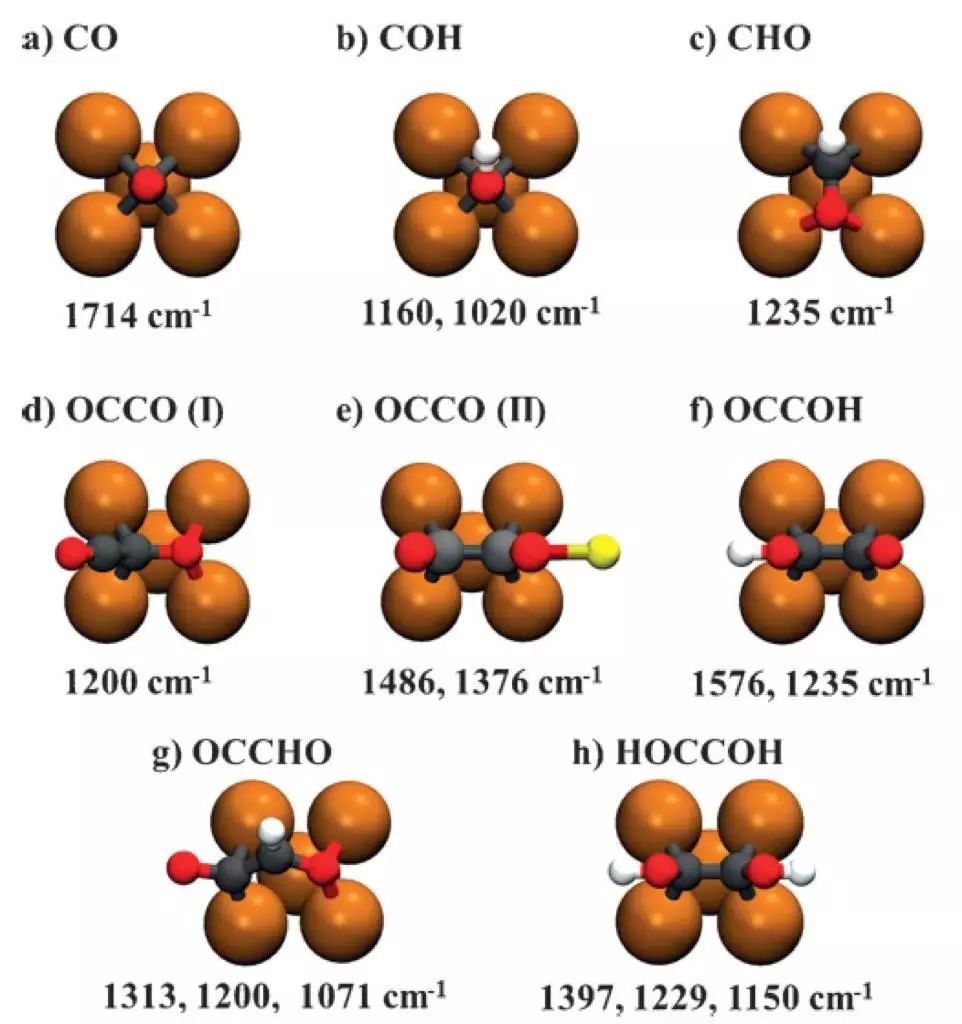
 图3. Cu(100)上会出现的不同吸附物及其构型的示意图。橘黄色的球代表Cu原子，深灰色的球代表C原子，红色的球代表O原子而白色的球代表H原子。每张图下面的振动频率是对应体系频率在1100-1600cm-1中的振动频率。通过仔细将计算结果与实验数据进行比对，作者可以说明从实验上观察到了C2 dimer的存在（由于振动频率与理论计算结果一致）。

【小编点评】：本文作者通过实验+理论的方式验证了CO在Cu(100)晶面上形成了CO-dimer的结构。虽然整个思路很简单，但是这样实验-理论互相应征的方法值得我们学习。并且作者选择了振动频率这个指标，在红外光谱上可以简单的测量，并且DFT计算也不是件难事。因此在实验-理论进行合作时，如何选择双方都轻松的指标显得尤为重要。如何抓住这个“桥梁”，是发好文章的关键所在。

 3. Science Jan. 6, Vol. 355, Issue 6320

【领域】：理论与计算化学 —> 密度泛函理论

【问题】：为什么密度泛函理论计算能量越来越精确而计算电荷密度越来越不准？ 

【方法】：（没有具体的方法，只是对密度泛函理论的发展历程进行了回顾） 

【结论】：（1）现代的泛函发展已经逐渐远离“寻找精确泛函”的道路（2）只通过参数拟合的泛函不能很好处理那些对电荷密度的精确度有高要求的物理量（例如电偶极距、电荷分布以及自旋密度）（3）我们可以在建立泛函的过程中适当加入一些约束，这样被认为可以提高泛函对电荷密度的处理（4）我们希望通过正确的方式得到正确的答案。（原文是：”most scientists would prefer to obtain the correct answerfor the correct reason”） 

【重要图例】：

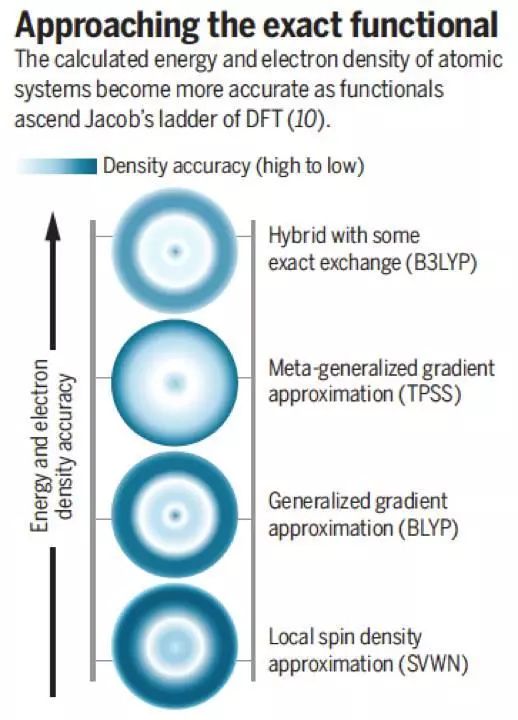
 图1. Jacob梯子（随着时间推移，泛函精确度会不断增加）。我们发现在能量精确度增加（TPSS—>B3LYP）时，电荷密度的精确度反而在降低（TPSS—>B3LYP）

【小编点评】：看来还是不能通过统计学的手段来硬性的“数据拟合”。这样从纯数学角度出发得到的结果往往会适得其反。抓住体系核心的物理条件、物理约束、物理本质，才是设计更好泛函的必经之路。 

在整个研究探索过程中，理论与实验的全方位合作对理解催化反应机理、高效催化剂的选择、催化剂设计等方面至关重要。