计算案例丨Sr-Zn系二元金属间化合物的结构、弹性和电子性质第一性原理研究

通过第一性原理平面波赝势法，我们计算了Sr-Zn系中二元金属间化合物的结构、弹性和电子性质。平衡结构参数与实验值符合。形成焓计算结果表明Sr-Zn系中所有的二元金属间化合物都是热力学稳定相结构并且都符合力学稳定性判据。

通过第一性原理平面波赝势法，我们计算了Sr-Zn系中二元金属间化合物的结构、弹性和电子性质。平衡结构参数与实验值符合。形成焓计算结果表明Sr-Zn系中所有的二元金属间化合物都是热力学稳定相结构并且都符合力学稳定性判据。首次利用单晶弹性常数结果去获得了这些金属间化合物的各向弹性性质和各向声速度。随着Zn原子含量的上升，Sr-Zn金属间的力学模量和理论硬度值增大。最后，分析了它们的电子态密度和原子电荷布居值以揭示这些金属间化合物内在的成键机制。

近年来，由于Sr-Zn二元系在技术领域的重要性得到了研究人员的广泛关注。Bruzzone等人通过热分析、X射线分析首次建立了Sr-Zn二元相图，并且被很好的采用了。后来报道了通过金相法和电动势法测得Sn元素在液态Zn中的溶解度。根据已有的Sr-Zn相图，存在四种金属间化合物，包括SrZn，SrZn2，SrZn5和SrZn13。其中SrZn5有两种相结构，分别为α-SrZn5 (Pnma) 和β-SrZn5 (P63/mmm)。关于这些金属间化合物的晶体结构已有相关报道，各自的晶体学信息也已经确定。很明显，它们可以被归类为极性金属间化合物。理论上，Zhong等人确定Sr-Zn系的热力学模型，它们的相图模型和前人的实验值符合。Spencer等人[11]报道了Sr-Zn系的形成焓值以及Ca-Zn系的热力学性质。到目前位置，很少有关于这类金属间化合物的力学和电子性质的报道。另外，一些零散的研究缺乏很好的一致性。材料基因组计划的主旨也是要获得各种材料的信息，包括晶体学和性能。因此，对这一类金属间化合物进行了一个系统的研究是非常有必要而且是具有很大的意义。基于密度泛函理论的第一性原理研究方法广泛的应用在各个领域。尤其对晶体结构材料的物理和化学性质的研究。在本文中，我们研究了SrZn，SrZn2，α-SrZn5，β-SrZn5和SrZn13这五种典型的Sr-Zn金属间化合物。许多性质的研究属于首次报道，这也是为后续的相关研究提供有力的理论支撑。

1、 模拟方法及参数设置

本论文中的计算都采用Material Studio软件中基于密度泛函理论的平面波赝势法的CASTEP模块。交换关联能采用广义梯度近似(GGA)中的PBE形式，使用Vanderbilt超软鹰势来描述离子实与价电子之间的相互作用，为了计算能满足计算的精度，平面波截断能取400.0eV，布里源区K点积分采用Monkhorst-Pack形式，SrZn，SrZn2，α-SrZn5，β-SrZn5和SrZn13的k点设置分别为6×11×8，10×6×6，4×7×10，10×10×12和4×4×4，自洽场运算时采用了Pulay密度混合法，并采用基集修正。自洽场的收敛精度取5×10-6eV/atom，每个原子上的力低于0.01 eV/Å，公差偏移低于5×10-4 nm，应力偏差低于0.02 GPa。以上参数能够满足收敛标准，参与计算的元素价电子为Sr (4s24p65s2)和Zn (3d104s2)，其它电子轨道当做芯层电子来处理。在能量计算和性质计算之前都采用BFGS方法对结构进行优化，得到稳定结构。

2、 模拟结果及讨论

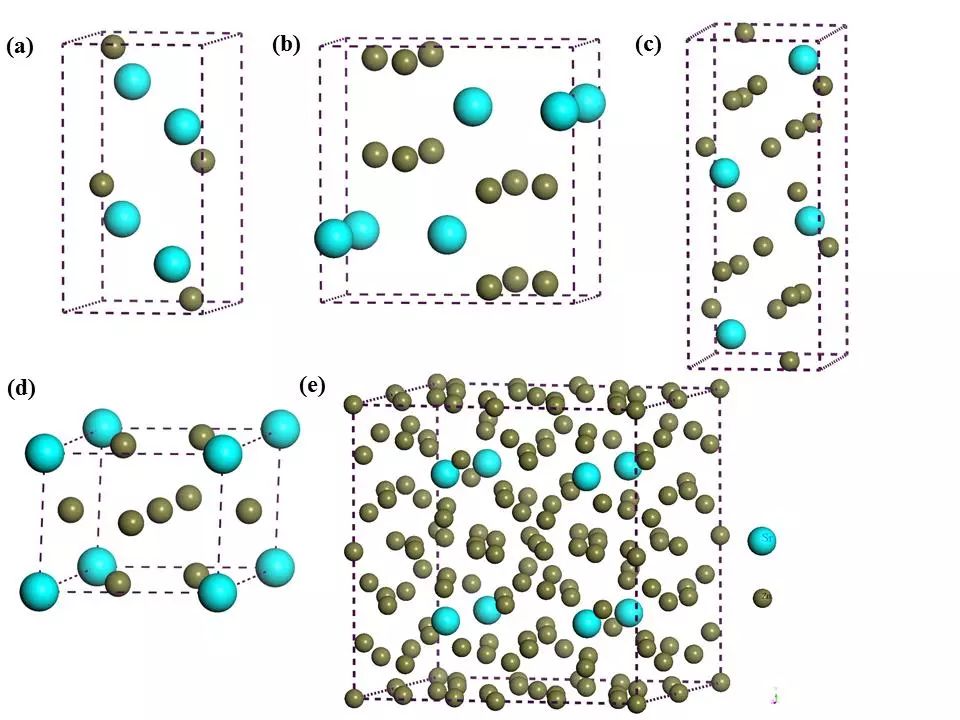
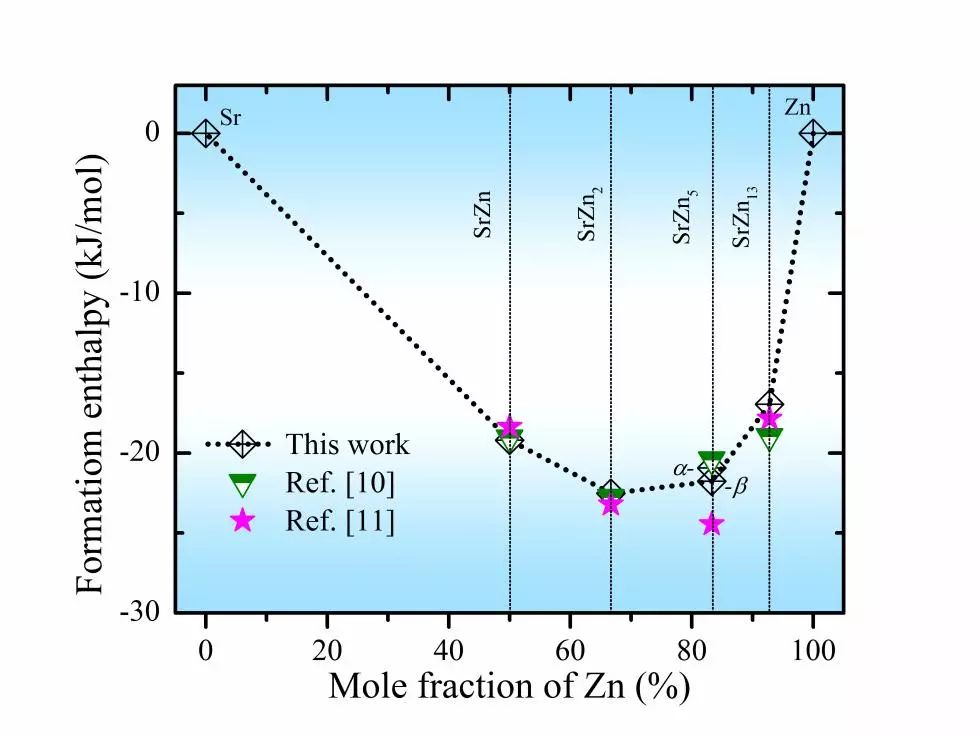
Sr-Zn中金属间化合物的晶胞模型作于图1，其中SrZn5晶体结构存在一个同质转变。为了得到这些化合物的平衡态晶格常数，我们进行了几何优化操作。结果表明，本文的理论值和前人报道的实验值非常接近，偏差都在1%之类。这说明本文选取的计算参数与交换关联泛函是可信的。理论晶格常数和实验值的偏差主要来自于温度效应的影响。为了测得这类化合物的热力学稳定性，我们计算了它们的形成焓大小。负的形成焓值表示该种结构的化合物在热力学上是稳定的。负值越大，晶体结构越稳定。为了更好的比较它们的相对稳定性大小，我们将计算得到的形成焓值作图于图2。首先，本文的计算值和参考文献[10]和[11]中的结果符合。从图中看到，所有的形成焓值都为负值，这表明所有的化合物都是热力学稳定的。其中，α-SrZn5的形成焓值比β-SrZn5的更低，这表明α-SrZn5更为稳定。同一种物质不同结构的化合物的稳定性差异来自于原子的堆垛方式的不同。稳定性大小排序为：SrZn2> α-SrZn5> β-SrZn5>SrZn> SrZn13。排序结果和Zhong等人[10]的研究结果一致。

图1 Sr-Sn二元金属间化合物的晶胞结构图，SrZn (a)，SrZn2 (b)，α-SrZn5 (c)，β-SrZn5 (d)和SrZn13(e)

图2 计算得到了Sr-Zn系二元金属间化合物的形成焓值，以及相关文献中的参考值

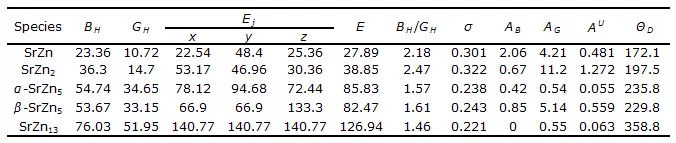
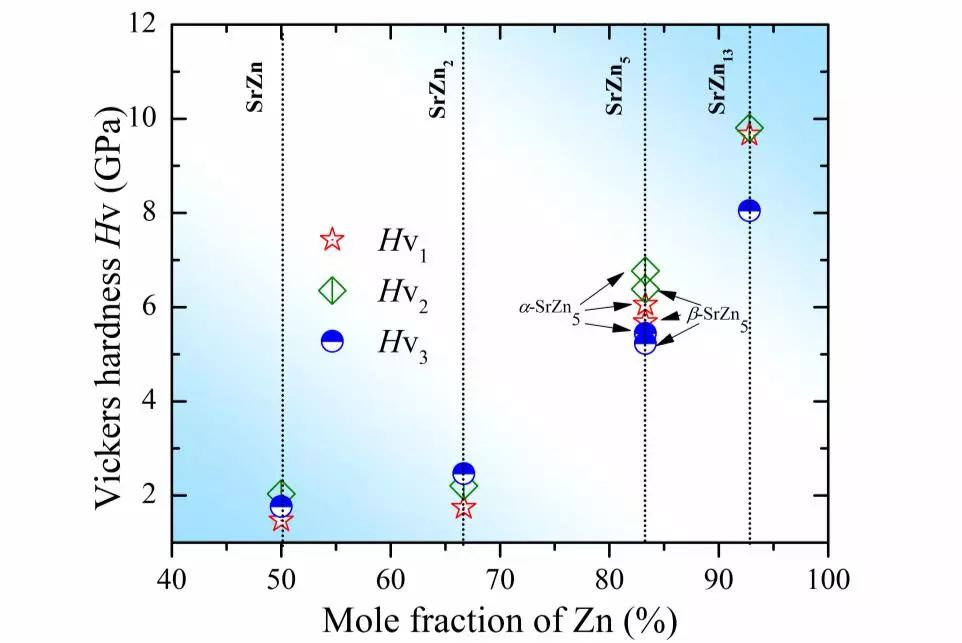
晶体的弹性常数可以通过第一性原理得到，首先对晶胞施加不同的弹性变形，然后通过弹性形变的能量与未变形晶胞的能量差求出弹性应变能，最终得到弹性常数。相同地，我们计算了这五种相结构的单晶弹性常数。结果表明：三种相结构的单晶弹性常数都满足各自晶系的力学稳定性条件。我们知道，单晶弹性常数对于合金或金属体系来说是非常有限的。由于实验条件和样品制备的困难，很难获得这类化合物的单晶弹性常数。因此，为了验证本次计算的弹性常数结果的准确性，我们计算了纯Sr和Zn单质的弹性常数，这样就可以和已有的实验值进行比对。结果表明纯Sr和Zn的单晶弹性常数和已有的实验值吻合较好，这进一步可以作证这五种金属间化合物弹性常数结果的可靠性。与单晶弹性常数相比，多晶力学模量往往有着更高的实际应用价值，通过VRH近似法，我们获得了这五种Sr-Zn金属间化合物的多晶力学模量，结果列于表1。体模量可以用来描述原子间的键强，从而表征体系的力学性质。从表1看到，Sr-Zn金属间化合物的体模量呈现增大的趋势。两种类型的SrZn5有着相似的体模量，这说明在它们中的原子键强是相近的。在图3中，我们看到SrZn，SrZn2，α-SrZn5，β-SrZn5和SrZn13的理论硬度值和体模量以及剪切模量线性相关。与β-SrZn5相比，α-SrZn5有着略微更高的理论硬度值，这和力学模量结果是相符的。

表1 通过Voigt-Reuss-Hill近似法得到的宏观力学模量、泊松比、各向异性指数和德拜温度

图3 通过不同理论公式获得的SrZn (a)，SrZn2 (b)，α-SrZn5 (c)，β-SrZn5 (d)和SrZn13 (e)的硬度值

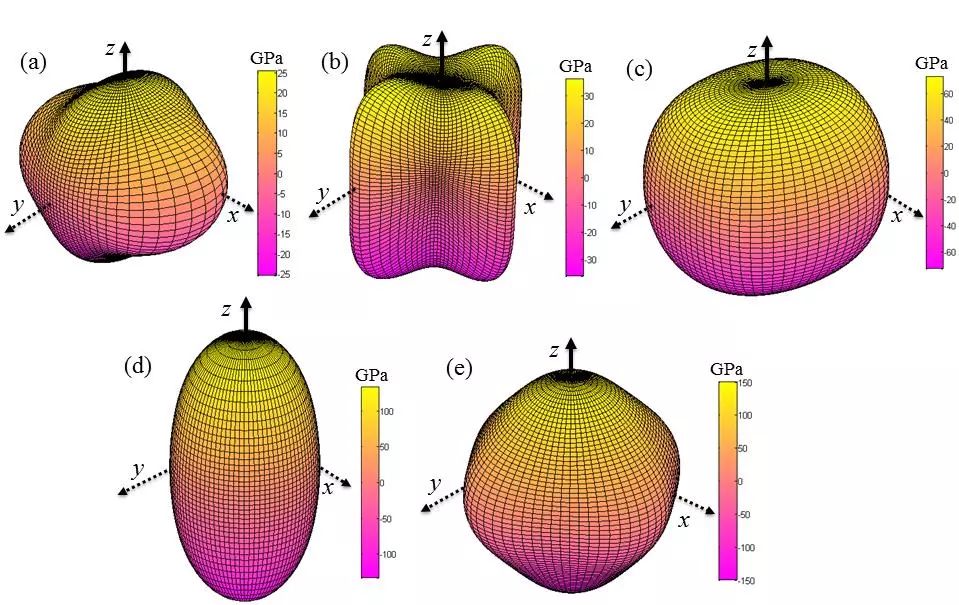
通过杨氏模量各向异性图，我们形象的描述了这五种化合物的力学各向异性(图4)。显然，五种化合物的杨氏模量3D图都显示不同程度的各向异性。SrZn2的各向异性程度最大，这和它有着最低的晶体对称性是分不开的。更重要的是，我们发现SrZn13的杨氏模量3D图并不是球形状的。我们往往会认为立方晶体的杨氏模量是各向同性的。在这里我们参考了经典文献[46]，解释了SrZn13体相为什么没有显示各向同性的特质，这是杨氏模量各向异性公式中的弹性柔度矩阵有关。

图4SrZn (a)，SrZn2 (b)，α-SrZn5 (c)，β-SrZn5 (d)和SrZn13 (e)杨氏模量3D图

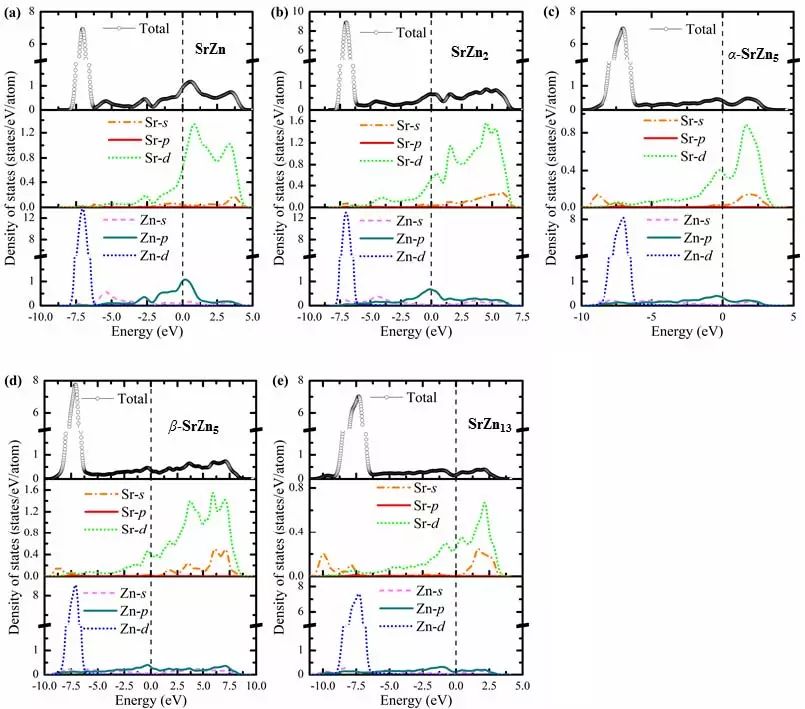
最后，我们分析了这五种金属间化合物的电子态密度，见图5。原则上讲，态密度可以作为能带结构的一个可视化结果。很多分析和能带的分析结果可以一一对应，很多术语也和能带分析相通。但是因为它更直观，因此在结果讨论中用得比能带分析更广泛一些。从图中我们可以看到在费米能级以上都存在态密度值，这表明了它们的金属特性。在低能级区域，从-10 eV到-5.0 eV，总态密度中的峰值主要来自于Zn的d态电子。高度局域性的d态电子和笔者之前研究的MgZn2相有着非常类似的现象。紧接着，从-5.0 eV到费米能级处的态密度主要来自Sr的d态和Zn原子的p态。表明这两者对该体系的金属行为有着重要的影响。在费米能级之上，整个总态密度图呈现一种低且肥大的一种形态，这和Zn原子的外层d轨道是密切联系的。另外，我们看到Sr原子钟的s-d态杂化，从而导致了共价键的存在。特别地，我们发现α-SrZn5中的原子杂化强度比β-SrZn5高，使得晶体结构的化学键强度存在差异，最终导致力学模量的差异。原子布居值结果表明，这五种晶体结构中都存在电荷的转移，暗示着离子键的存在。综上所述，SrZn，SrZn2，α-SrZn5，β-SrZn5和SrZn13金属间化合物是共价键、离子键和金属键的混合体。

图5 计算得到的SrZn (a)，SrZn2 (b)，α-SrZn5 (c)，β-SrZn5 (d)和SrZn13 (e)电子态密度图

3、 结论

采用第一性原理研究方法，我们获取了Sr-Zn系二元金属间化合物的结构稳定性，力学各向异性和电子结构。结果表明，这五种化合物在热力学和力学上都是稳定结构。α-SrZn5的形成焓值比β-SrZn5的更低，表明它有着更高的结构稳定性。它们的力学模量和理论硬度值随着Zn原子浓度的上升呈现上升的趋势。根据B/G判据，SrZn和SrZn2被认为是延展性相，其它三种为脆性相。立方结构SrZn13的杨氏模量3D他呈现各向异性，这是经典文献中的描述是一致的。电子态密度结果表明，五种化合物的力学模量差异可能来自于晶体结构中的Zn的原子的d态电子的宽化行为。这些结果都属于首次报道，具有很好的理论指导作用。

本文作者：胡文成1，刘勇1，李克1，金华兰1，徐春水1，李德江2，曾小勤3；1）南昌大学江西省高性能确成形重点实验室，2）上海交通大学轻合金精密成型国家工程研究中心，3）上海交通大学金属基复合材料国家重点实验室

本文转载自创腾学院，转载目的在于知识分享，本文观点不代表V-suan云平台立场。