能带结构图、态密度图的基本分析方法

色散图和DOS图一般也就长这样

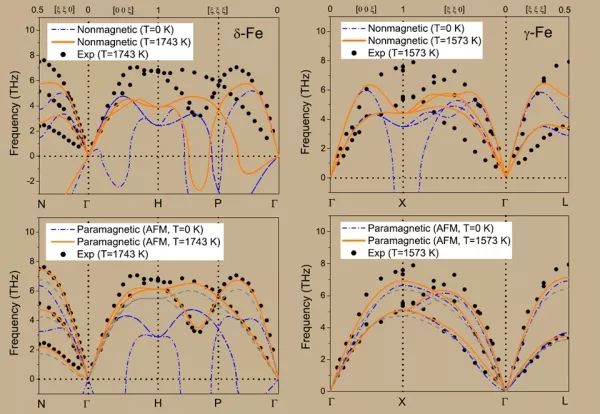
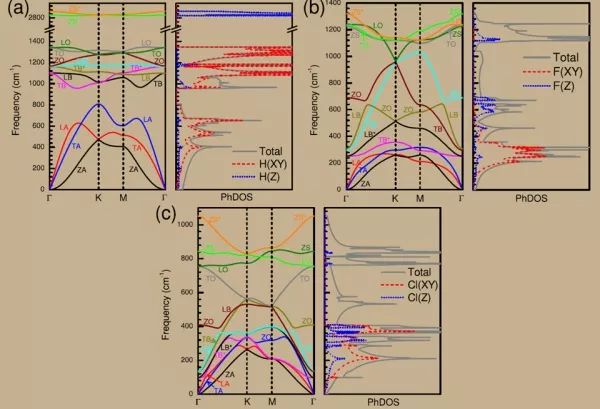
不光电影有3D的，态密度也有3D

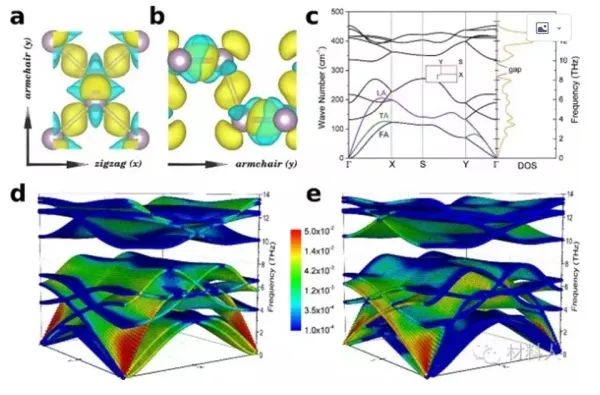
（a）顶视图和（b）侧视图，其中的黄色表示电荷累积，青色相反。

（c）声子谱和态密度。面外的横波光学声子模式（TOz）在布里渊区中心区域软化预示着强非简谐性。

（d，e）三维声子谱。

那么我想很多人要问什么是声子谱，什么是对称点

查书、查书、查书

态密度

定义：态密度就是单位频率间隔内的状态数（振动模式数目），表示为：

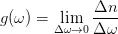
一维情况下的态密度

一维情形，波矢空间单位长度上的模式数为L/2pi。当L很大时，点是准连续的，对于任意间隔dq，q在这一间隔中的模数为：

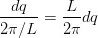
频率在(w，w+dw)范围内的模数，可以通过色散关系给出。由态密度的定义得到，

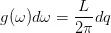
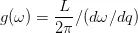
好了，到现在，我们差不多知道了 g(w) 是怎么来的了。

只要知道色散关系，就有了态密度。

那么色散关系不用再解释了吧

一维单原子链的色散关系

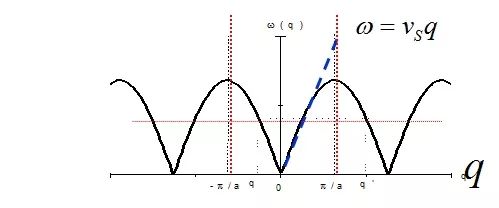
这个色散关系从哪里来？

将晶格振动简化为简谐振动，然后求解微分方程就得到上图的色散关系。

对于三维晶体的态密度和声子谱，将一维的结论稍微扩展一下就可以啦。

那么态密度有啥用？

有了态密度，我们差不多就有了一切。

很多时候分布比数量来的重要，一个女人性感不性感，关键要看肉是长在胸部还是长在脸上，而不是她的体重。所以呀，分布决定性状。

同样，对于一个物理体系，能量分布很重要。能量分布决定了体系的状态或者材料的性能。统计力学中，我们常会遇到配分函数，配分函数的实质就是能量的分布。能量分配方式—>配分函数->体系的熵和自由能->体系的状态。态密度实际上也就对应着能量分布，有了态密度，我们就可以根据统计力学得到想要的热力学量(hongguanxingzhi)。

众骚年们，在这里，我得提一下，虽说态密度很强悍，但态密度不是你想算，想算就能算。只有一部分体系是可以算的，可以算的这些体系也是很难算的。

________________________________________________ ______________

下面接着说能带

简述一下能带论

孤立原子中电子的分立能级

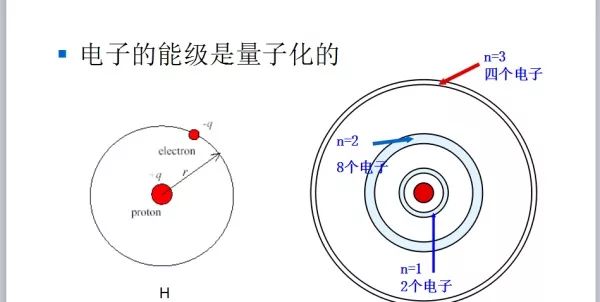
多原子系统电子能级的分裂

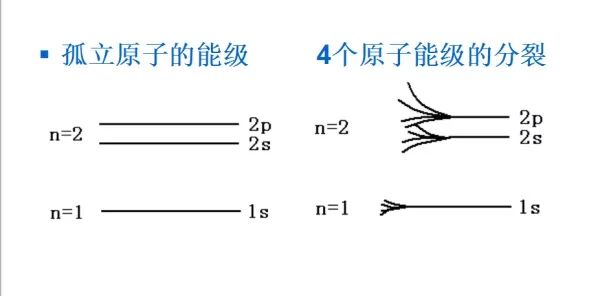
留给你们一个问题：多原子体系能级为啥要分裂？

一维能带结构扩展布里渊区表示

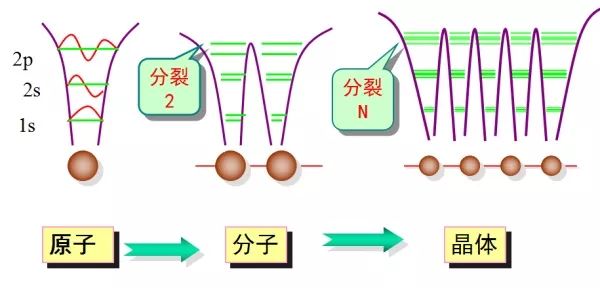
上面那个问题没人回答啊，我就再补一张图

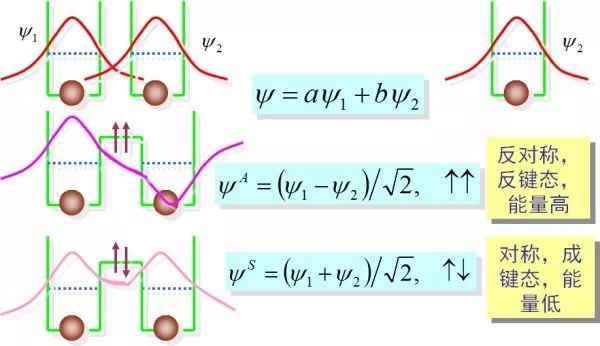
金属、半导体和绝缘体的能带结构

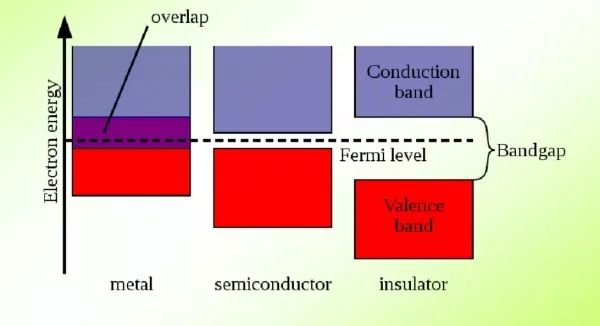
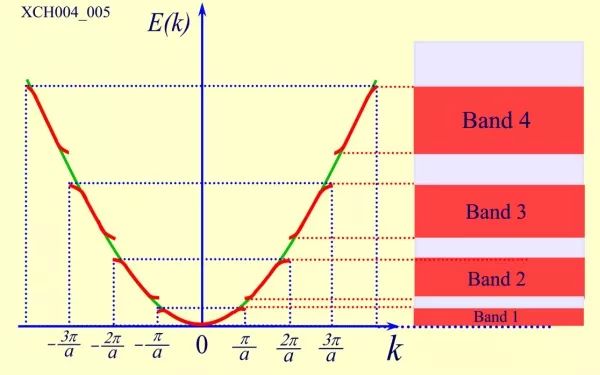
在单原子中电子能级是分立的，这一点是基于量子力学的描述，否则按照经典物理描述能级就是连续的。在晶体中，由多个原子的共同作用使得单能级分裂为N个能级，看起来这些能级就像连续分布的的，我们就叫它能带。于是我们才有了价带、导带、禁带的概念。

再来看看文献中的能带图

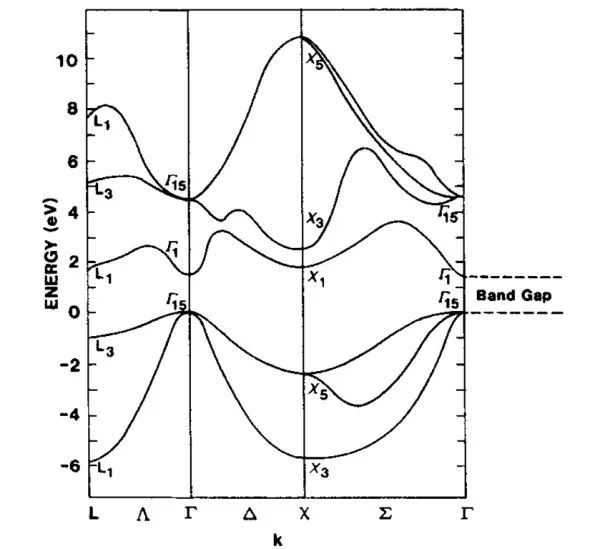
这个和上面那个图没有什么区别，只不过这时晶体（三维格子）的能带图，之上的是一维的。这也是一个色散图，只不过是个能量—波矢图。

______ _____________________________________________________

实际上除了dos，energy band，还有charge density.

但总的来说都离不开分布

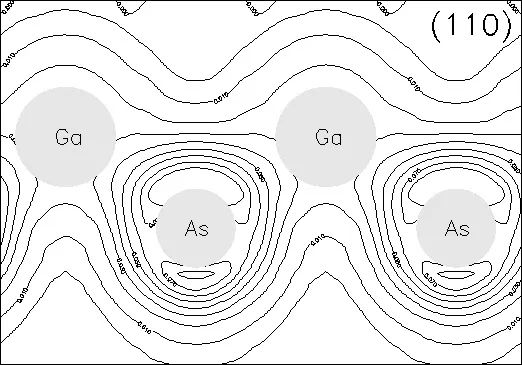
还不懂，就认真看固体物理。固体物理看不懂，赶紧回头看统计力学和量子力学。

————————————————————————————————————

能带图的横坐标是在模型对称性基础上取的K点。为什么要取K点呢？因为晶体的周期性使得薛定谔方程的解也具有了周期性。按照对称性取K点，可以保证以最小的计算量获得最全的能量特征解。能带图横坐标是K点，其实就是倒格空间中的几何点。纵坐标是能量。那么能带图应该就是表示了研究体系中，各个具有对称性位置的点的能量。我们所得到的体系总能量，应该就是整个体系各个点能量的加和。

主要是从以下三个方面进行定性/定量的讨论： 1、电荷密度图（charge density）； 2、能带结构（Energy Band Structure）； 3、态密度（Density of States，简称DOS）。

电荷密度图是以图的形式出现在文章中，非常直观，因此对于一般的入门级研究人员来讲不会有任何的疑问。唯一需要注意的就是这种分析的种种衍生形式，比如差分电荷密图（def-ormation charge density）和二次差分图（difference charge density）等等，加自旋极化的工作还可能有自旋极化电荷密度图（spin-polarized charge density）。所谓“差分”是指原子组成体系（团簇）之后电荷的重新分布，“二次”是指同一个体系化学成分或者几何构型改变之后电荷的重新分布，因此通过这种差分图可以很直观地看出体系中个原子的成键情况。通过电荷聚集（accumulation）/损失（depletion）的具体空间分布，看成键的极性强弱；通过某格点附近的电荷分布形状判断成键的轨道（这个主要是对d轨道的分析，对于s或者p轨道的形状分析我还没有见过）。分析总电荷密度图的方法类似，不过相对而言，这种图所携带的信息量较小。

成键前后电荷转移的电荷密度差。此时电荷密度差定义为：delta_RHO = RHO_sc – RHO_atom 其中 RHO_sc 为自洽的面电荷密度，而 RHO_atom 为相应的非自洽的面电荷密度，是由理想的原子周围电荷分布堆彻得到的，即为原子电荷密度的叠加(a superposition of atomic charge densities)。需要特别注意的，应保持前后两次计算（自洽和非自洽）中的 FFT-mesh 一致。因为，只有维数一样，我们才能对两个RHO作相应的矩阵相减。

能带结构分析现在在各个领域的第一原理计算工作中用得非常普遍了。首先当然可以看出这个体系是金属、半导体还是绝缘体。对于本征半导体，还可以看出是直接能隙还是间接能隙：如果导带的最低点和价带的最高点在同一个k点处，则为直接能隙，否则为间接能隙。

1）因为目前的计算大多采用超单胞（supercell）的形式，在一个单胞里有几十个原子以及上百个电子，所以得到的能带图往往在远低于费米能级处非常平坦，也非常密集。原则上讲，这个区域的能带并不具备多大的解说/阅读价值。因此，不要被这种现象吓住，一般的工作中，我们主要关心的还是费米能级附近的能带形状。

2） 能带的宽窄在能带的分析中占据很重要的位置。能带越宽，也即在能带图中的起伏越大，说明处于这个带中的电子有效质量越小、非局域（non-local）的程度越大、组成这条能带的原子轨道扩展性越强。如果形状近似于抛物线形状，一般而言会被冠以类sp带（sp-like band）之名（此陈述有待考证—博主加）。反之，一条比较窄的能带表明对应于这条能带的本征态主要是由局域于某个格点的原子轨道组成，这条带上的电子局域性非常强，有效质量相对较大。

3）如果体系为掺杂的非本征半导体，注意与本征半导体的能带结构图进行对比，一般而言在能隙处会出现一条新的、比较窄的能带。这就是通常所谓的杂质态(doping state)，或者按照掺杂半导体的类型称为受主态或者施主态。

4） 关于自旋极化的能带，一般是画出两幅图：majority spin和minority spin。经典的说，分别代表自旋向上和自旋向下的轨道所组成的能带结构。注意它们在费米能级处的差异。如果费米能级与majority spin的能带图相交而处于minority spin的能隙中，则此体系具有明显的自旋极化现象，而该体系也可称之为半金属（half metal）。如果majority spin与费米能级相交的能带主要由杂质原子轨道组成，可以此为出发点讨论杂质的磁性特征。

5）做界面问题时，衬底材料的能带图显得非常重要，各高对称点之间有可能出现不同的情况。具体地说，在某两点之间，费米能级与能带相交；而在另外的k的区间上，费米能级正好处在导带和价带之间。这样，衬底材料就呈现出各项异性：对于前者，呈现金属性，而对于后者，呈现绝缘性。因此，有的工作是通过某种材料的能带图而选择不同的面作为生长面。具体的分析应该结合试验结果给出。

原则上讲，态密度可以作为能带结构的一个可视化结果。很多分析和能带的分析结果可以一一对应，很多术语也和能带分析相通。但是因为它更直观，因此在结果讨论中用得比能带分析更广泛一些。

简要总结分析要点如下：

1） 在整个能量区间之内分布较为平均、没有局域尖峰的DOS，对应的是类sp带（此陈述有待考证—博主加），表明电子的非局域化性质很强。相反，对于一般的过渡金属而言，d轨道的DOS一般是一个很大的尖峰，说明d电子相对比较局域，相应的能带也比较窄。

2）从DOS图也可分析能隙特性：若费米能级处于DOS值为零的区间中，说明该体系是半导体或绝缘体；若有分波DOS跨过费米能级，则该体系是金属。此外，可以画出分波（PDOS）和局域（LDOS）两种态密度，更加细致的研究在各点处的分波成键情况。

3）从DOS图中还可引入“赝能隙”（pseudogap）的概念。也即在费米能级两侧分别有两个尖峰。而两个尖峰之间的DOS并不为零。赝能隙直接反映了该体系成键的共价性的强弱：越宽，说明共价性越强。如果分析的是局域态密度（LDOS），那么赝能隙反映的则是相邻两个原子成键的强弱：赝能隙越宽，说明两个原子成键越强。上述分析的理论基础可从紧束缚理论出发得到解释：实际上，可以认为赝能隙的宽度直接和Hamiltonian矩阵的非对角元相关，彼此间成单调递增的函数关系。

4） 对于自旋极化的体系，与能带分析类似，也应该将majority spin和minority spin分别画出，若费米能级与majority的DOS相交而处于minority的DOS的能隙之中，可以说明该体系的自旋极化。

5）考虑LDOS，如果相邻原子的LDOS在同一个能量上同时出现了尖峰，则我们将其称之为杂化峰（hybridized peak），这个概念直观地向我们展示了相邻原子之间的作用强弱。

由于金属的能带有可能穿越fermi能级，从而引起总能计算时的不连续变化。为了避免这种情况，需要引入分数的占据态smearing。

本文转载自知乎，转载目的在于知识分享，本文观点不代表V-suan云平台立场。