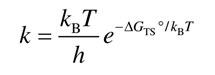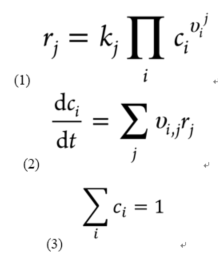理论计算中的微观动力学，来看这些催化反应路径有多美！

本文经授权转载自研之成理（ID：rationalscience）

本文为理论化学研习社的第一篇文章。化学反应动力学能为催化机理带来重要的认识。

小编按：本文为理论化学研习社的第一篇文章。化学反应动力学能为催化机理带来重要的认识。反应速率，活化能等实验值的测量提供了与理论计算的桥梁。因此，理论计算的微观动力学能给实验研究者带来更多的动力学信息。

前言： 

随着计算机性能提高，计算程序逐渐成熟，用计算手段辅助实验已经逐渐成为高水平表面催化文章的标配。

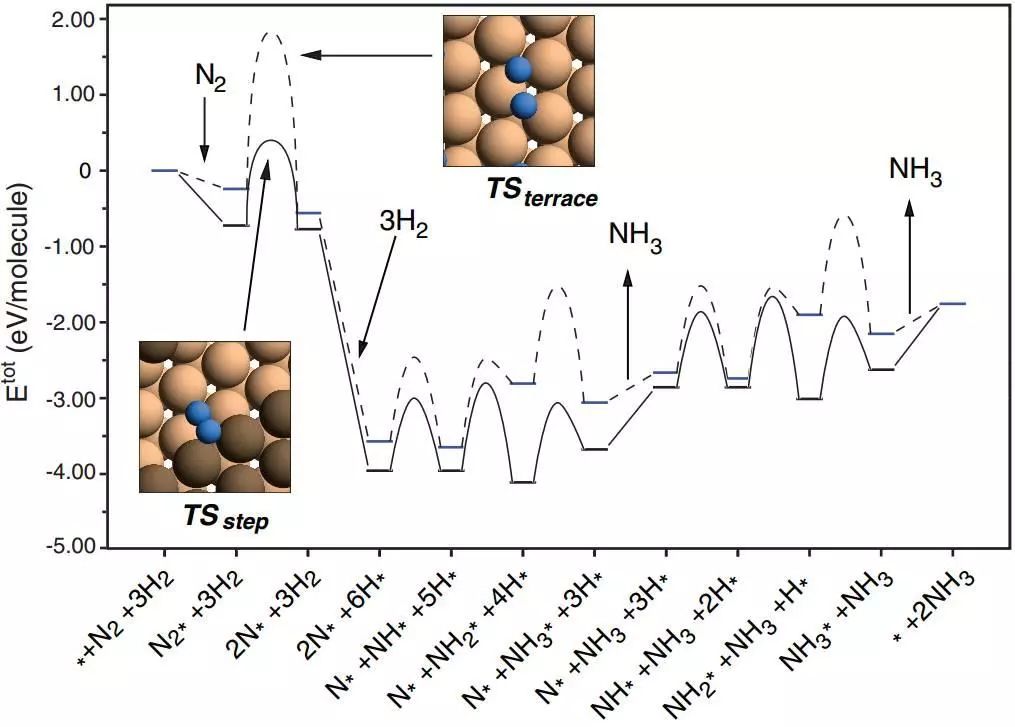
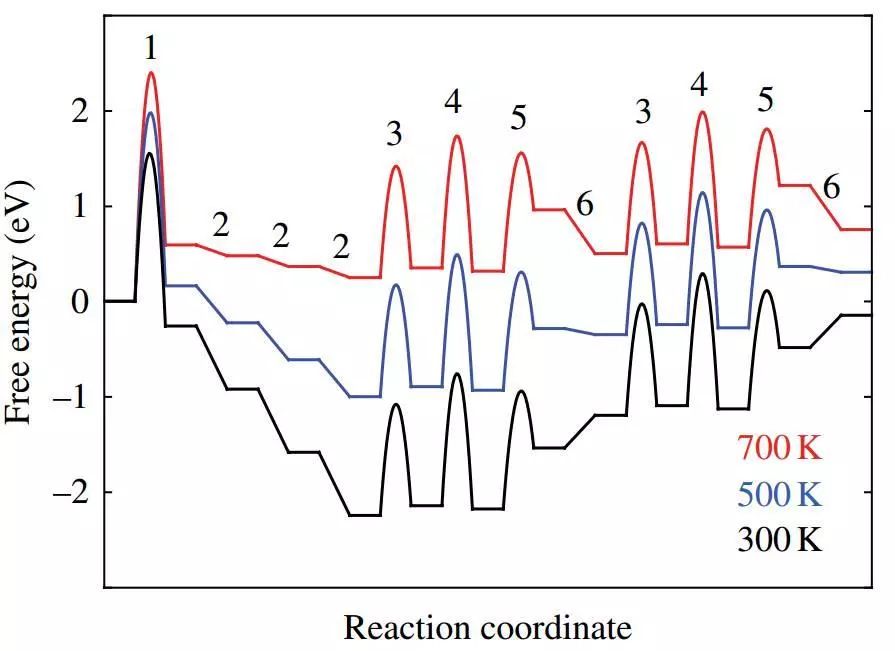
其中最常见的就是图一这样反应路径和过渡态计算。这样的反应路径看起来很美好，但是怎么才能从这些能量数据里获取有效信息来解释催化剂活性/选择性，甚至是预测新的催化剂。解微观动力学方程直接计算反应turnover Frequency（TOF）就成为简单且优雅的手段。下面我们就以合成氨反应为例，展示微观动力学方法原理（图一）。

图一. 合成氨反应势能面：虚线是密堆积的Ru(0001)面，实线是Ru台阶位置的B5 site。B5 site由五个Ru原子组成，downstairs上的3-fold位点和upstairs的2个Ru。

 背景介绍：

20世纪初期，德国的弗里茨·哈伯（Fritz Haber）和卡尔·博施(Carl Bosch) 开发出了将大气中的氮转化为可提供营养的氨的第一个实用过程：催化合成氨。而在哈伯过程发现之前，氨一直难以在工业规模上生产。合成氨工艺是人工化肥的生产支柱，是人类生存发展的“食”之基础，不论是在基础理论研究还是实际工业应用方面都被物理化学家广泛的关注和研究。迄今为止，Nobel奖曾3次颁发给合成氨相关领域的科学家（图二）。

图二. 合成氨相关诺贝尔奖获得者（从左到右）：Fritz Haber(1918)；Carl Bosch(1931)；Gerhard Ertl(2007)。

 合成氨反应机理：

A)   合成氨的基元反应

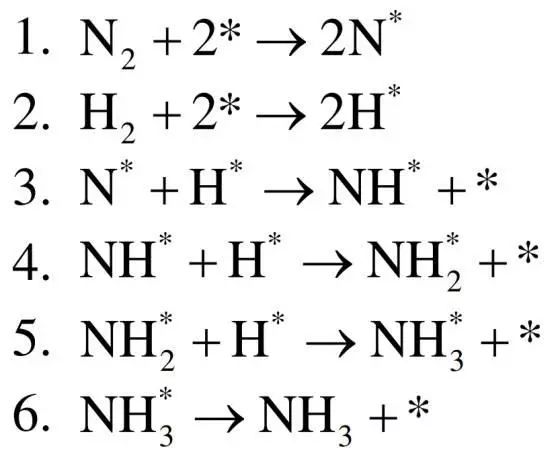
在金属表面上催化合成氨有六个基元反应步骤，分别是N2解离吸附，氢气解离吸附，三步加氢反应和氨气脱附：

B)   理论计算做些什么？

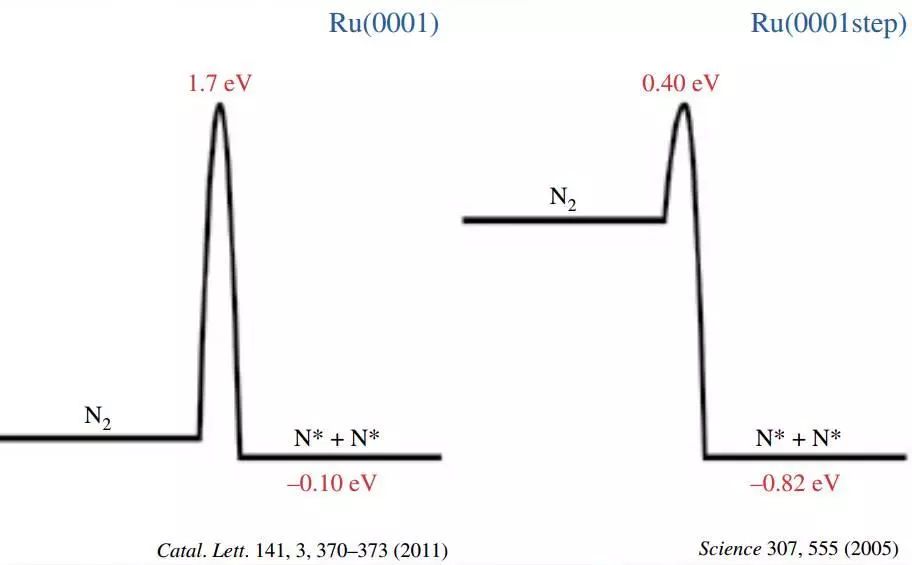
定性分析：大部分实验/计算合作的文章一般通过理论计算得出每个基元反应正向和逆向反应的能垒和能量变化（这些能量都是在0 K下，并且忽略零点振动能的能量，可以由VASP, Dmol3, Quantum ESPRESSO, ABINIT, CASTEP,FHI-aims, CP2K等软件完成，之后我们可能会有VASP使用的专题讲解）。然后根据反应能垒对催化剂的活性和选择性做一些定性分析，比如下图，*N2在Ru B5 site（step位？）的解理吸附能垒比在密堆积的（0001）面上低1.3 eV,所以氮气活化肯定在B5 site上要快。但是，具体催化反应能快多少，是不是能垒和反应能越低越好，气体温度压力对反应速率的影响都需要做进一步反应动力学分析。

图三. *N2在Ru B5 site / 密堆积的（0001）面的解理吸附能垒和反应能量变化。

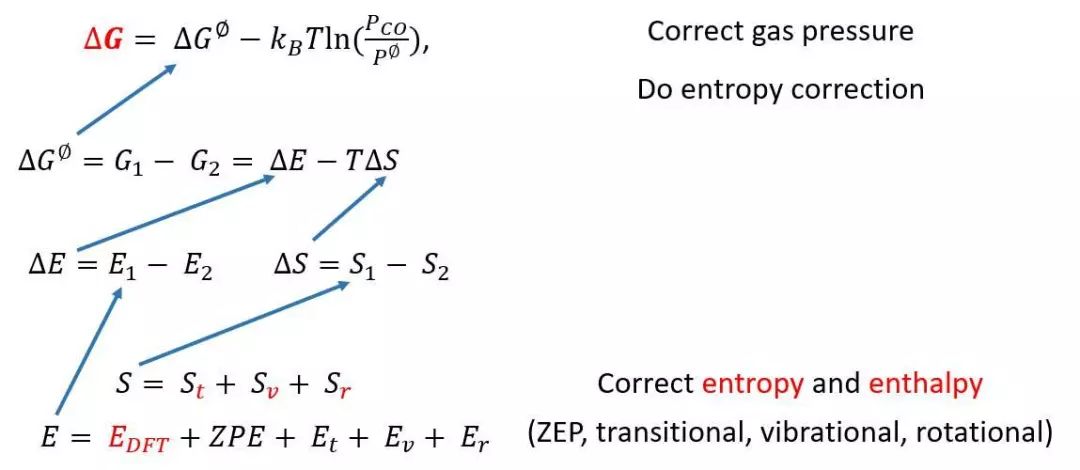
微观动力学计算：而想要从DFT计算结果得到实际条件下的反应速率就需要先计算每个基元反应的自由能变和自由能能垒。图四里E(DFT)就是0 K下的能量，具体步骤：1）首先需要校正零点振动能（ZPE）; 2）然后分别计算每个中间体的平动/振动/转动配分函数，从而得到平动能/振动能/转动能(Et/Ev/Er) 和平动熵/振动熵/转动熵(St/Sv/Sr); 3) 再通过E-T*S就可以计算出在温度T和一个标准大气压下的自由能; 4)最后再校正实际反应条件下的压力就可以得到在实际反应条件下所有中间体的自由能G。（具体过程参考傅献彩《物理化学》统计热力学一章）

图四. 由DFT计算得到的能量计算自由能

图五， Ru B5 site自由能反应势能面，对应于图一实线的DFT能量path。

       下面问题就变成如何由自由能G计算反应速率常数k了：

       过程十分简单，用过渡态的G(transition state)减去初态G(initial state)就得到-ΔG(ts)，代入上面公式就能得到每个基元反应正逆过程的反应速率k。然后就是基于稳态近似（所有中间体覆盖度不变）和平均场近似（吸附物种的周围环境不影响反应能量变化）列微观动力学方程，一共有三种等式：

（1）     反应速率方程。r是速率，k是速率常数，c是物种覆盖度, v是化学计量, *是表面空位点；比如合成氨反应的第一个基元步：r1 = k1[N2][*]2；r-1 = k-1[N*]2

（2）     基于稳态近似的等式：比如[N*]的覆盖保持不变则d[N*]/dt = r1 – r-1 – r3+ r-3

（3）     限制表面总覆盖度的等式: [*] + [N*] + [HN*] + [H2N*] + [H3N*]= 1

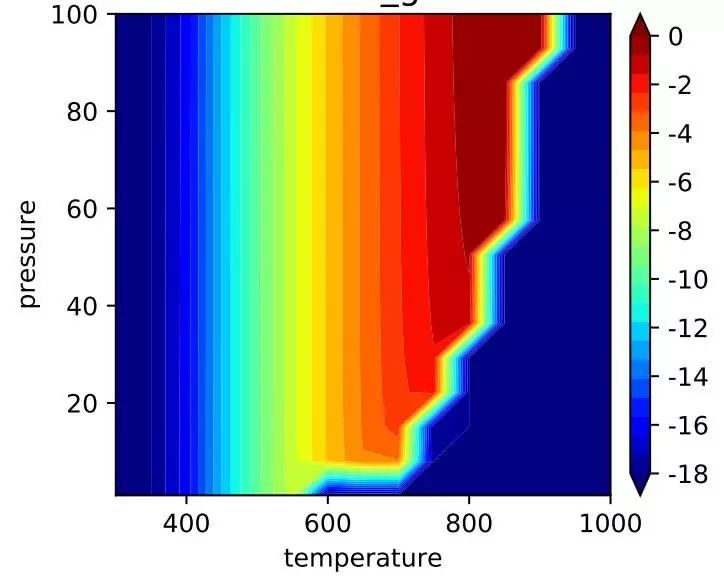
然后就是解微分方程了，可以使用matlab或者python编程，之后我们还会介绍CatMap解微观动力学。这样我们就会得到在一定温度T，压力P下的某个位点上的每个物种的覆盖度c，最后把c再代回公式(1)就能得到每个反应的速率r。从r可以计算得到总的反应TOF，而根据每个反应路径所占比重可以分析选择性。如果对每个温度点/压力点解微观动力学方程，就能画出log(TOF) map：如图六。

图六，在300-1000 K, 1-100 bar 下的Ru B5 site 的log(TOF) 图，在高温高压下反应速率最高，但是超过一定温度，速率降为0，此时发生氨分解反应。

后记：

事实上，微观动力学的所有基本原理在物理化学课程中都已经学过，但是简单的内容所发挥出来的效果确实炫酷。微观动力学是处理表面催化反应的利器，对于提升表面计算催化工作水平，深入分析催化过程具有重要的意义，同时也是连接理论计算和实验的桥梁

本文转载自研之成理（ID：rationalscience），转载目的在于知识分享，本文观点不代表V-suan云平台立场。