计算催化前沿 | J. K. Nørskov：利用理论计算来设计新的固体催化剂

本文经授权转载自研之成理

【前言】

书读百遍，其义自见！最近又重读了下Nørskov的这篇综述（Nature Chem. 2009, 1, 37-46），简单地将论文中的一些核心观点梳理下分享给大家，希望对大家有所帮助。论文标题： Towards the computational design of solid catalysts, DOI: 10.1038/nchem.121.

【背景介绍】

A. 基本原则：催化剂的催化性能本质上都是由其电子结构决定的，因此催化剂的设计从根本上来说是要综合考虑组成，物理结构等因素来调控材料的电子结构。

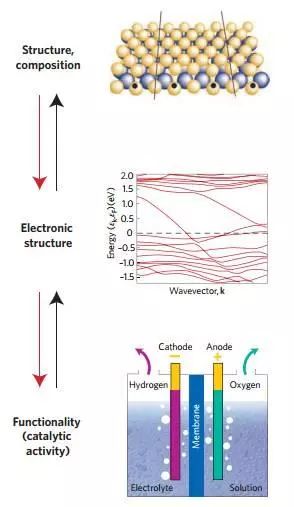
Figure 1

B. 目前理论计算的主要出发点：为什么这个催化剂能够表现出优异的性能？（验证型）

C.实际需求：给定催化反应条件，如何知道需要哪种材料？（探究型）

简单地来说，理论计算最基本的一个发展路线就是如何从验证发展到探究，如何从证明发展到预测。只有当理论计算真正实现预测的时候，才能算是理论计算的成熟期。

【催化活性的趋势（trends）和描述因子（descriptors）】

理论计算简化实际催化体系的基本方法：将催化剂简化为一个个相互独立的晶面，所有的表面都会对催化反应有所贡献，而贡献最大的就是主要的活性中心。

对于一个催化反应而言，找到一个衡量催化剂活性的descriptor以及明确不同催化剂的活性趋势是非常重要的，这是理解催化剂结构性能关系以及利用理论计算预测催化剂的基础。

为什么在理论计算中总是会看到一些火山图？

注意，火山图一般出现在多步反应途径中。这其实跟过渡态的稳定性有关系，某一过渡态比较稳定的话，形成这个过渡态就比较容易（势垒较低），但相应地从这个过渡态变到另一个状态就会困难一些（势垒会更高）；而相反，若过渡态的稳定性较差的话，形成中间体会很困难（势垒较高），而变到另一个状态会比较容易（势垒会比较低）。所以，多步骤反应中会经常存在这样的平衡（Sabatier principle）。

这里作者举了个例子：CO+3H2–CH4+H2O, 其中CO的解离以及CH4+H2O的生成就存在这样的一个平衡，如果CO解离成C+O在催化剂表面很稳定，那么形成CH4+H2O的势垒就会比较高，而相反则解离比较困难，这种平衡的存在不可避免的就会出现一个火山型曲线，如Figure 3C所示。

其实得到火山型曲线是比较简单的，问题是采用怎样的descriptor来将这个催化过程的规律体现出来。这里之所以采用CO的解离能是因为根据BEP原则，CO解离成C+O的活化能跟CO解离能之间是线性相关的（Figure 3b），所以可以用CO的解离能作为descriptor，说明的规律就是刚才说的那个平衡。

备注：BEP原则（Bell–Evans–Polanyi principle）的表达式Ea=Eo+αΔH。其中ΔH是反应的焓变，Ea是反应活化能，Eo和α是特征参数。

类似的其实在电化学析氧（OER）反应中，通常采用的descriptor是ΔG(O)*-ΔG(HO)*，请查阅：ChemCatChem 2011, 3, 1159 – 1165.

【催化剂电子结构的描述因子】

比较经典的是d-band模型，而这个也正是Norskov所提出来的：the higher in energy the d-states are relative to the highest occupied state- the Fermi energy- of the metal, the stronger the interaction with adsorbate states.

具体的例子大家看下图就知道了

在OER催化中，Yang Shao-Horn课题组(Science, 2011,334,1383)曾提出：The filling of the surface transition metal antibonding states of eg-orbital parentage is a more appropriate descriptor for catalysis.

【催化剂的设计】

其实原理上很简单，在得到了一个火山型曲线之后（Figure 3C），火山型曲线峰值所对应的肯定是最好的，但是很多情况下这些材料都比较贵，比如CO+3H2—CH4+H2O这个反应而言，最好的催化剂Ru和Co都挺贵的，那么如何设计一个便宜一点的催化剂呢？一个基本的原则就是从火山曲线的两边选择材料来进行复合（合金化），比如说Ni和Fe，一个在左支，一个在右支，通过复合可以让其性能变得更好，具体如下图所示。

【催化选择性】

 催化选择性一般用不同反应路径的势垒差来进行衡量，势垒差越大选择性越高。以乙烯的环氧化为例，它的中间态可以是环氧乙烷也可以是乙醛，生成环氧乙烷的话就会直接脱附，而生成乙醛则会进一步深度氧化。The difference in energy between these two transition states thus becomes a good descriptor for the selectivity of an EO catalyst, and catalysts, which favour the transition state going towards EO, can be sought computationally. 从Figure 7可以看出，加入一定量的Cu可以提高Energy difference，因此可以提高选择性（当然这里也要考虑一个问题，就是到底谁更容易生成的问题，所要优化的应该是更容易生成EO的催化剂）。

备注:文章讲到了好几个例子，刚兴趣的朋友自己去查看原文哈

【难点与展望】

1. 对于催化剂的设计而言，除了高活性，选择性，低成本这些可以用于计算的性能指标外，催化剂稳定性，抗中毒性等等也是非常重要的参数，而这些在理论计算中并不能全面覆盖到。

2. DFT计算的结果应该跟催化反应条件紧密结合起来，以合成氨为例，氨气浓度不一样，理想的催化剂就会不一样，低氨气浓度下Fe最优，高氨气浓度下Ru最优。

3. 如何将催化剂的载体有效地纳入到计算的范畴中？

 总的来说，理论计算仍处在发展阶段，不过目前结合原位表征手段，DFT计算来研究催化反应机理已经成为了主流，如何进一步完善理论计算，最终实现理论指导实践是个漫漫求索的过程！

在整个研究探索过程中，理论与实验的全方位合作对理解催化反应机理、高效催化剂的选择、催化剂设计等方面至关重要。